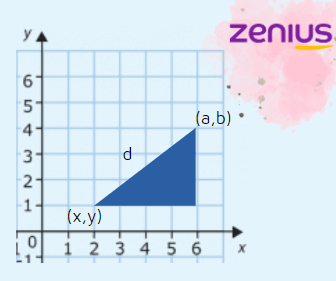
Bentuk segitiga. Dari situ diketahui alas dan tingginya berapa, kemudian hitung sisi miringnya menggunakan rumus teorema pythagoras.
d = akar dari delta x^2 + delta y^2
Maka harus mencari Δx dan Δy terlebih dahulu. Caranya seperti ini:
(Δx)2=(x-a)2
(Δy)2=(y-b)2
Sehingga, bisa dituliskan juga rumus phytagorasnya:
d = akar dari (x-a)^2 + (y-b)^2
d^2 = (x-a)^2 + (y-b)^2
"Lingkaran adalah kumpulan titik-titik pada bidang datar (dua dimensi) dan memiliki jarak yang sama terhadap suatu titik pusat."
Nah, jarak antara suatu titik dan titik pusat disebut jari-jari lingkaran. Sedangkan, garis yang terbentang dari titik ujung ke titik ujung lainnya melalui titik tengah disebut diameter. Jadi, diameter itu dua kali ukuran jari-jari lingkaran.
Ada lagi nih yang namanya tali busur, yaitu garis yang terbentang dari suatu titik ke titik lainnya tanpa melalui titik tengah.
Mencari jari jari bisa menggunakan konsep seperti pada pythagoras sebelumnya. Jika diminta untuk mencari jari-jari lingkaran yang terbentang dari titik (a,b) ke titik (x,y), maka dapat menggunakan teorema pythagoras.
Buat dulu bentuk segitiga siku-sikunya. Kemudian, hitung menggunakan teorema pythagoras seperti ini:
r = akar dari (x-a)^2 + (y-b)^2
Namun ada dua aturan yang perlu dipahami dari suatu bentuk persamaan lingkaran, yaitu pusat (0,0) dan (a,b) dengan masing-masingnya berjari-jari r.
Jika suatu lingkaran memiliki pusat (0,0) dengan jari-jari r, maka bentuk persamaannya x2+y2=r2.
Jika suatu lingkaran memiliki pusat (a,b) dengan jari-jari r, maka bentuk persamaannya
(x-a)2+(y-b)2=r2.
x2+y2+Ax+By-C=0
Tentukan persamaan lingkaran dengan pusat (1,2) dan memiliki jari-jari 5. Tentukan persamaan lingkarannya!
Jawab:
p = (1,2) → pusat lingkaran (a,b)
r = 5
Karena pusat lingkarannya (a,b), maka kita gunakan aturan (x-a)2+(y-b)2=r2.
(x-a)2+(y-b)2=r2
(x-1)2+(y-2)2=25
Selanjutnya, konversi bentuk standar ini ke dalam bentuk umumnya:
x2-2x+1+y2-4y+4=25
x2+y2-2x-4y-20=0
Sehingga, bentuk umum persamaan lingkaran dengan pusat (2,3) dan jari-jari 5 adalah x2+y2-2x-4y-20=0.